Multiobjective Optimization
In this crashworthiness optimization example more than one criteria will be considered as objective function. Hence the solution is not unique, but will result in a Pareto optimal front. The same model is considere here using a single objective approach.
The problem is of a simplified vehicle moving at a constant velocity and crashing into a pole.
 |
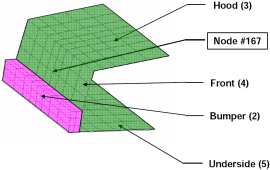 |
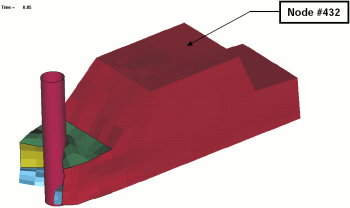
| Fig. 1(a): Deformed vehicle after 50 ms | Fig. 1(b): Design variables with part numbers |
The problem illustrates the following features:
|
The criteria of interest are the following:
Design variables:
|
Design Formulation
The design formulation is as follows:
- Minimize the Mass and Intrusion subject to HIC (15ms) < 250. The intrusion is measured as the distance between the nodes 167 and 432 (for the location of the nodes see Fig. 1).
