Welcome to LS-OPT Support Site...

LS-OPT, the graphical optimization tool that interfaces perfectly with LS-DYNA, allows the user to structure the design process, explore the design space and compute optimal designs according to specified constraints and objectives. The program is also highly suited to the solution of system identification problems and stochastic analysis. The graphical tool LS-OPTui interfaces with LS-DYNA and provides an environment to specify optimization input, monitor and control parallel simulations and post-process optimization data, as well as viewing multiple designs using LS-PREPOST.

Collection of documents related to LS-OPT, Optimization and Stochastics

Examples

This section demonstrates LS-OPT capabilities by means of a series of examples.

HowTos

Collection of information and examples for several tasks with LS-OPT

FAQs

FAQ's related to Optimization, Robustness and Reliability Analysis

Videos

Tutorial videos

News

Site News

Welcome to LS-OPT Support Site

Optimization

LS-OPT is designed to meet all requirements to solve arbitrary non-linear optimization tasks.

Successive Response Surface Method (SRSM)

Very effective algorithm for highly nonlinear problems such as crashworthiness or metal forming applications

Genetic Optimization Algorithm (GA)

suitable for arbitrary problems in particular for complex performance functions
(e.g. many local minima)

Multidisciplinary Optimization (MDO)

More than one load case and more than one CAE-Discipline
Parallel execution of multiple load cases with different analyzing types and possibly different variable definitions
Discipline-specific job control
Discipline specific point selection schemes (experimental design)

Multi-Objective Optimization

Simultaneous optimization of more than one objective function
Pareto Front Solutions

Reliability Based Design Optimization (RBDO)

Optimization that directly accounts for the variability and the probability of failure

Robust Design Optimization (RDO)

Optimizing design and robustness simultaneously

Optimization variables

Continuous and discrete variables
Mixed discrete-continuous optimization
Dependent (linked) variables

Identification of system-/material parameters

Calibration of models to experimental data

Shape optimization

Process of optimizing the geometrical dimensions of a structural part
Interface to parametric pre-processors: ANSA, HyperMorph, TrueGrid, User-Defined

Examples:

back to Home

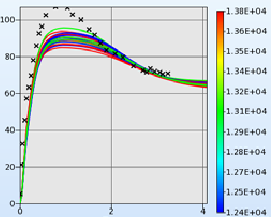
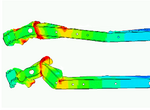
System-/Parameter Identification

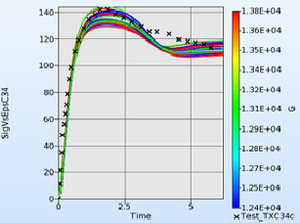
The utilization of new materials such as plastics, composites, foams, textile or high-strength steels require the application of highly complex material models. These material models generally bring along numerous material parameters, which are difficult to define. The optimization program LS-OPT is excellently suited for the identification of these parameters. By the parameterized simulation of the physical tests with LS-DYNA an automated calibration to the test results is performed. The objective is to minimize the error between the test results and the simulation results.

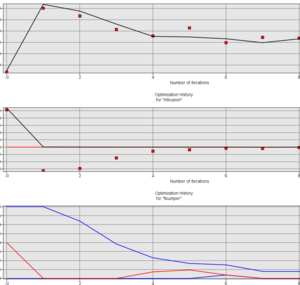
Optimization Algorithm

Successive Response Surface Method (SRSM)

Calibration of

Scalar values
Global curves
Full-field calibration

Curve Extraction

Interface to LS-DYNA output
Target curve from file
Interface to gom/ARAMIS
Crossplots

Curve matching metrics

Mean Squarred Error
Curve Mapping (e.g. for hysteretic curves)
Dynamic Time Warping

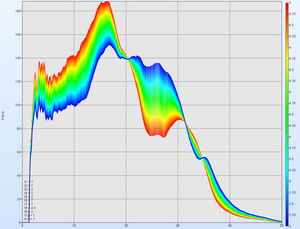
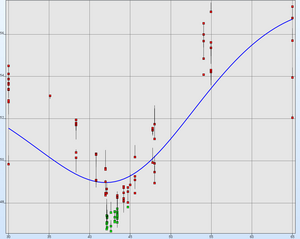
Visualization

History Plot
Visualization of simulated and target curve
LSPP fringe plots

Examples:

back to Home

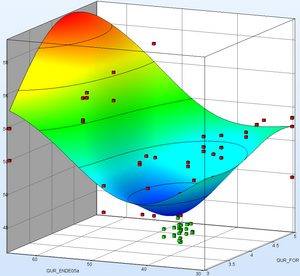
Design Exploration

LS-OPT allows global approximations of the design space using meta models. These meta models may be used for design exploration.

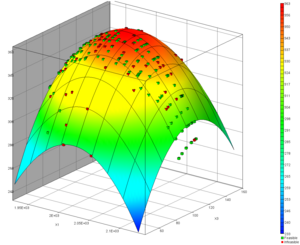
Response Surfaces (Meta Models)

Global approximation of Responses and Histories
Metamodel types: Polynomials, Radial Basis Functions, Feedforward Neural networks

Visualization

2D/3D sections of the surfaces
- 1/2 selected variables vs. any response
Constraints on the meta models
Influence of single parameter on a history curve
Interactive prediction of response values

Examples:

Crashworthiness Optimization - Linear Response Surface with Strategy Single Stage

back to Home

Sensitivity Studies

Methods for the determination of significant variables are implemented in LS-OPT.

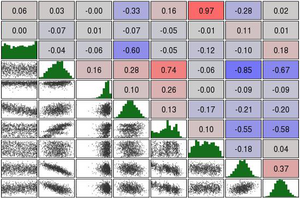
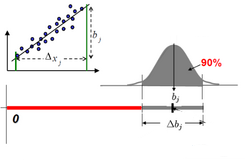
Linear ANOVA (Analysis of Variance)

regression based method
evaluated on metamodel
90% confidence interval
normalized with respect to design space
influence of variables on single response

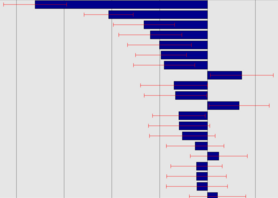
Global Sensitivity Analysis (Sobol)

variance based method
evaluated on metamodel
nonlinear for nonlinear metamodel
normalized
absolute value
determination of influence of variables an multiple responses or on the whole problem possible

Examples:

back to Home

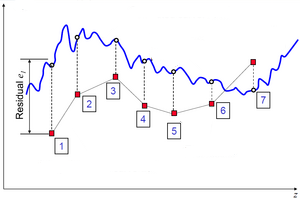
Robustness Analysis

Stochastic methods and features for robustness analysis are implemented in LS-OPT.

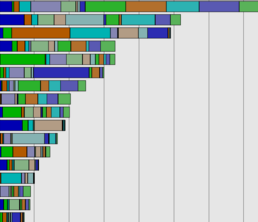
Monte Carlo Investigations

Direct and metamodel based
Estimation of Mean, Std. Deviation
Correlation Analysis
Confidence Intervals
Outlier Analysis
Stochastic contribution analysis

Reliability studies

Determination of failure probability
Methods: FOSM, FORM

Reliability Based Design Optimization

Optimization that directly accounts for the variability and the probability of failure

Robust Design Optimization

Optimizing design and robustness simultanously

Visualization of statistical results on the FE-Model (DYNAstats)

Fringe of mean and standard deviation on the FE-model utilizing LS-PrePost
Display of variation of element results such as stress, thinning, plastic strain...
Correlation of node displacements with respect to any response
Statistics of time history curves

Examples:

back to Home

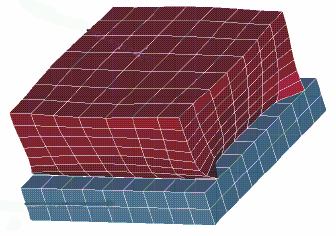
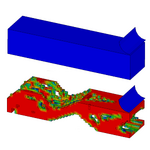
Topology Optimization

LS-TaSC™ is a Topology and Shape Computation tool. Developed for engineering analysts who need to optimize structures, LS-TaSC works with both the implicit and explicit solvers of LS-DYNA. LS-TaSC handles topology optimization of large non-linear problems, involving dynamic loads and contact conditions.

General capabilities

Solid design using first-order hexahedrons and tetrahedral elements
Shell design using first-order quadrilateral and triangular elements
Global constraints
Multiple load cases, e.g. static, impact and NVH
Tight integration with LS-DYNA
Large models with millions of elements

Geometry definitions

Multiple parts
Symmetry
Extrusions
Casting, one sided
Casting, two sided
Forging

Postprocessing

Design histories
LS-PrePost plots of the geometry evolution and the final design
Iso-surfaces

back to Home

Imprint

The following company contributes to this web site:

Anschrift
DYNAmore GmbH, an Ansys Company
Zentrale
Industriestraße 2
D-70565 Stuttgart

Telefon
+49 (0)711-459600-0

Telefax
+49 (0)711-459600-29

E-Mail
E-Mail an DYNAmore

Webseite
www.dynamore.de

Geschäftsführer
Richard Belcher

Florian Vogel

Registergericht
Stuttgart

Sitz
Stuttgart

Registernummer
HRB 765839

Umsatzsteuer-Identifikationsnummer (gemäß § 27 a Umsatzsteuergesetz)
DE320033770

Welcome to LS-OPT Support Site

LS-OPT, the graphical optimization tool that interfaces perfectly with LS-DYNA allows the user to structure the design process, explore the design space and compute optimal designs according to specified constraints and objectives. The program is also highly suited to the solution of system identification problems and stochastic analysis.

DYNAmore.png

**Click to view full-size image…** Size: 1KB