Creating imperfections in LS-DYNA® using the *PERTURBATION keyword

Imperfections for buckling and other instability problems can be created in LS-DYNA® using the *PERTURBATION keyword. These imperfections and perturbations are also known as stochastic fields. Modeling these imperfections is crucial for instability problems such a buckling analysis.

The intended class of problems is those problems whose results depend on getting the imperfections or initial conditions correct. Modeling the observed imperfections and stochastic fields correctly is an important step in getting the mechanics correct, which in turn will allow analysts to validate more results in the realm of unstable and stochastic behavior.

LS-DYNA includes a general ability to create stochastic fields from correlation functions.
Three types of imperfections are currently implemented:

Geometric imperfections. Buckling analysis is done using geometric imperfections.
Variation of a shell thickness. This currently mostly used for robustness analysis of metal forming problems where the change in thickness is due to the rolling process.
The stochastic variation of material properties.

There are three methods of creating a stochastic field:

Specifying a correlation function via parameters.
Specify it as a sum of sine waves (a Fourier expansion).
Specify it directly for every element or node.

Additionally, these perturbations can be created in coordinate systems and scaled.

Using correlation functions to create a random field

This is a very general method of creating stochastic fields and can create quite a variety of random fields.
This methodology requires that a correlation function be specified as shown in Figure 1 and Figure 2. The figures also show how different stochastic fields are created for the different types of stochastic fields and different values of the parameters.

willem_1

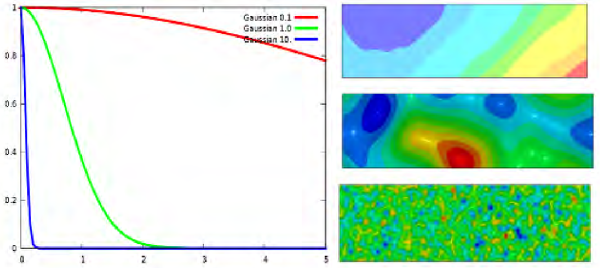
Figure 1 This figure shows how the correlation distance affects the different stochastic fields that can be obtained. Decreases in the width of the Gaussian correlation functions results in more fine-grained stochastic fields.

willem_2

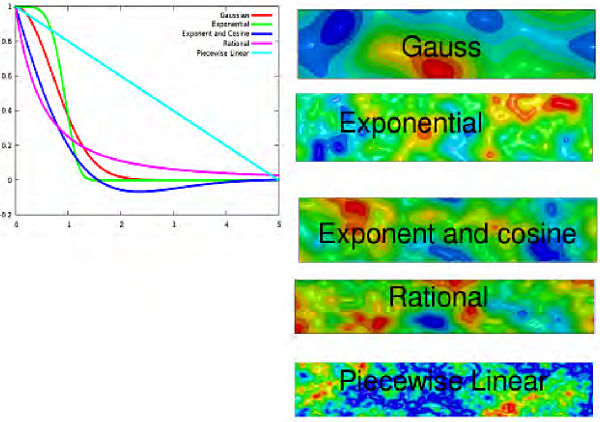
Figure 2 This figure shows how the different perturbations that can be obtained from different types of correlation functions.

Additionally, Figure 3 shows how the properties of the stochastic field can differ in different directions.

willem_3

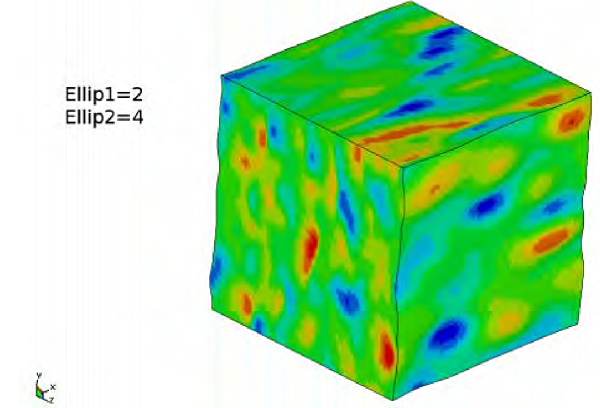
Figure 3 The stochastic properties does not have to be the same in all directions. This figure shows a stochastic field with properties that are different in the x, y, and z directions. This is controlled using parameters.

Specification using sine waves

Sinusoidal imperfections can be added together to specify the final imperfection. In Figure 4 we show how this was done for to simulate a metal forming blank. See also Reliability Based Design Optimization with LS-OPT® for a Metal Forming Application by Müllerschön, Lorenz & Roll, Frankenthal, 2007 for more information regarding the stochastic simulation of metal forming problems.

willem_4

Mill chatter Non-uniform roll contact

Figure 4 This example shows how two sinusoidal imperfections were added to simulate the variation in a metal forming blank due to the rolling of the steel.

Direct specification of a random field

The values of the stochastic field can be specified directly. For element thicknesses this is done using the existing *ELEMENT_SHELL_THICKNESS card; for nodal locations the stochastic field can be read in directly.
Two interesting cases can be distinguished:

The values can be LS-DYNA® results exported using LS-PREPOST® – this allows the use, for example, of a summation of the eigen modes to be used as a perturbation.
Alternatively, one can use this capability to make the shape changes for shape optimization.

Summary

Stochastic fields are provided in LS-DYNA® for problems whose behavior depends on these imperfections or initial conditions. This should allow the further validation of results in the realm of unstable and stochastic behavior. Modeling the observed imperfections and stochastic fields is required to get the mechanics correct in these cases.